TRIGONOMETRIA
L a trinometria es la rama de la matematica cuyo significado etimologico es la medicion de los triangulos, dervada en terminos griergos
La trigonometria se encarga de calcular los elementos de los triangulos para esto se encarga de estudiar las raliciones entre los angulos...
CIRCULO TRIGONOMETRICO
El circulo trigonometrico tiene la ventaja de ser una herramienta para etica en el manejo de los conceptos de trigonometria pero al mismo tiempo es un apoyo teórico, pues ayuda a fundamentar y tener una idea precisa de las funciones trigonométricas
FUNCION CUADRATICA
En matemáticas, una función cuadrática o función de segundo grado es una función polinómica definida como
gráficas de funciones cuadráticas.
en donde a, b y c son números reales (constantes) y a es distinto de 0.
La representación gráfica en el plano cartesiano de una función cuadrática es una parábola, cuyo eje de simetría es paralelo al eje de las ordenadas. La parábola se abrirá hacia arriba si el signo de a es positivo, y hacia abajo en caso contrario. El estudio de las funciones cuadráticas tiene numerosas aplicaciones en campos muy diversos, como por ejemplo la caída libre o el tiro parabólico.
La derivada de una función cuadrática es una función lineal y su integral una función cúbica.
ECUACIONES DE SEGUNDO GRADO
Una ecuación de segundo grado o ecuación cuadrática es una ecuación algebraica de segundo grado.1 2 Es decir que la mayor potencia de la incógnita considerada en la ecuación, es dos. La expresión general de una ecuación cuadrática es
donde x representa la variable y a, b y c son constantes; a es un coeficiente cuadrático (distinto de 0), b el coeficiente lineal y c es el término independiente.
La gráfica de una función cuadrática es una parábola. La ecuación cuadrática proporciona las intersecciones de la parábola con el eje de las abscisas, que pueden ser en dos puntos, en uno o ninguno.
L a trinometria es la rama de la matematica cuyo significado etimologico es la medicion de los triangulos, dervada en terminos griergos
La trigonometria se encarga de calcular los elementos de los triangulos para esto se encarga de estudiar las raliciones entre los angulos...
CIRCULO TRIGONOMETRICO
El circulo trigonometrico tiene la ventaja de ser una herramienta para etica en el manejo de los conceptos de trigonometria pero al mismo tiempo es un apoyo teórico, pues ayuda a fundamentar y tener una idea precisa de las funciones trigonométricas
FUNCION CUADRATICA

En matemáticas, una función cuadrática o función de segundo grado es una función polinómica definida como
gráficas de funciones cuadráticas.
en donde a, b y c son números reales (constantes) y a es distinto de 0.
La representación gráfica en el plano cartesiano de una función cuadrática es una parábola, cuyo eje de simetría es paralelo al eje de las ordenadas. La parábola se abrirá hacia arriba si el signo de a es positivo, y hacia abajo en caso contrario. El estudio de las funciones cuadráticas tiene numerosas aplicaciones en campos muy diversos, como por ejemplo la caída libre o el tiro parabólico.
La derivada de una función cuadrática es una función lineal y su integral una función cúbica.
ECUACIONES DE SEGUNDO GRADO
Una ecuación de segundo grado o ecuación cuadrática es una ecuación algebraica de segundo grado.1 2 Es decir que la mayor potencia de la incógnita considerada en la ecuación, es dos. La expresión general de una ecuación cuadrática es
donde x representa la variable y a, b y c son constantes; a es un coeficiente cuadrático (distinto de 0), b el coeficiente lineal y c es el término independiente.
La gráfica de una función cuadrática es una parábola. La ecuación cuadrática proporciona las intersecciones de la parábola con el eje de las abscisas, que pueden ser en dos puntos, en uno o ninguno.
METODO ANALITICO
Método Analítico: Este método implica el análisis (del griego análisis, que significa descomposición), esto es la separación de un tono en sus partes o en sus elementos constitutivos. Se apoya en que para conocer un fenómeno es necesario descomponerlo en sus partes.Método Sintético: Implica la síntesis (del griego synthesis, que significa reunión), esto es, unión de elementos para formar un todo.El juicio analítico implica la descomposición del fenómeno, en sus partes constitutivas. Es una operación mental por la que se divide la representación totalizadora de un fenómeno en sus partes.
El juicio sintético
por lo contrario, consiste en unir sistemáticamente los elementos heterogéneos de un fenómeno con el fin de reencontrar la individualidad de la cosa observada. La síntesis significa la actividad unificante de las partes dispersas de un fenómeno. Sin embargo, la síntesis no es la suma de contenidos parciales de una realidad, la síntesis añade a las partes del fenómeno algo que sólo se puede adquirir en el conjunto, en la singularidad.
PROGRESIONES
Método Analítico: Este método implica el análisis (del griego análisis, que significa descomposición), esto es la separación de un tono en sus partes o en sus elementos constitutivos. Se apoya en que para conocer un fenómeno es necesario descomponerlo en sus partes.Método Sintético: Implica la síntesis (del griego synthesis, que significa reunión), esto es, unión de elementos para formar un todo.El juicio analítico implica la descomposición del fenómeno, en sus partes constitutivas. Es una operación mental por la que se divide la representación totalizadora de un fenómeno en sus partes.
El juicio sintético
por lo contrario, consiste en unir sistemáticamente los elementos heterogéneos de un fenómeno con el fin de reencontrar la individualidad de la cosa observada. La síntesis significa la actividad unificante de las partes dispersas de un fenómeno. Sin embargo, la síntesis no es la suma de contenidos parciales de una realidad, la síntesis añade a las partes del fenómeno algo que sólo se puede adquirir en el conjunto, en la singularidad.
PROGRESIONES
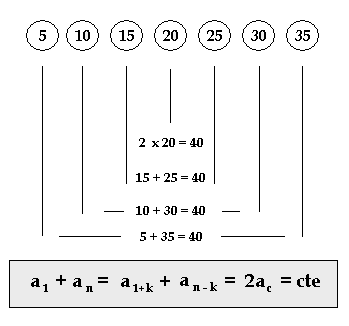
En matemáticas, una progresión aritmética es una serie de números tales que la diferencia de dos términos sucesivos cualesquiera de la secuencia es una constante, cantidad llamada diferencia de la progresión o simplemente diferencia o incluso "distancia".
Por ejemplo, la sucesión 3, 5, 7, 9, 11,... es una progresión aritmética de constante (o diferencia común) 2. Así como: 5 ; 2 ; -1 ; -4 es una progresión aritmética de constante "-3".
El término general de una progresión aritmética es aquel en el que se obtiene cualquier término sumándole la diferencia al término anterior. El término de una progresión aritmética es la expresión que nos da cualquiera de sus términos, conocidos alguno de ellos y la diferencia de la progresión. La fórmula del término general de una progresión aritmética es
INTERPOLACIONES
La palabra interpolar que equivale a intercalar, insertar,… quiere decir, tratándose de números, a situarlos, intercalarlos, entre otros dos.Veamos ejemplo práctico.Supongamos que nos dicen que entre 6 y 10 tenemos que interpolar o intercalar 3 términos y que además, tanto el 6 como el diez y los tres números que han de estar entre ellos, se encuentren en progresión aritmética.
Así que, decimos que son medios porque están entre otros dos y aritméticos por tratarse de progresiones aritméticas.
Debes fijarte, muy bien, que si te dicen que entre el valor 6 y el valor 10 debes interpolar 3 números o medios aritméticos, la nueva progresión tendrá 5 términos: el de valor 6, valor 10 y los tres nuevos.
La palabra interpolar que equivale a intercalar, insertar,… quiere decir, tratándose de números, a situarlos, intercalarlos, entre otros dos.Veamos ejemplo práctico.Supongamos que nos dicen que entre 6 y 10 tenemos que interpolar o intercalar 3 términos y que además, tanto el 6 como el diez y los tres números que han de estar entre ellos, se encuentren en progresión aritmética.
Así que, decimos que son medios porque están entre otros dos y aritméticos por tratarse de progresiones aritméticas.
Debes fijarte, muy bien, que si te dicen que entre el valor 6 y el valor 10 debes interpolar 3 números o medios aritméticos, la nueva progresión tendrá 5 términos: el de valor 6, valor 10 y los tres nuevos.
GEOMETRIA ANALITICA
La geometría analítica estudia las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas. Su desarrollo histórico comienza con la geometría cartesiana, impulsada con la aparición de la geometría diferencial de Carl Friedrich Gauss y más tarde con el desarrollo de la geometría algebraica. Actualmente la geometría analítica tiene múltiples aplicaciones más allá de las matemáticas y la ingeniería, pues forma parte ahora del trabajo de administradores para la planeación de estrategias y logística en la toma de decisiones.
La geometría analítica estudia las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas. Su desarrollo histórico comienza con la geometría cartesiana, impulsada con la aparición de la geometría diferencial de Carl Friedrich Gauss y más tarde con el desarrollo de la geometría algebraica. Actualmente la geometría analítica tiene múltiples aplicaciones más allá de las matemáticas y la ingeniería, pues forma parte ahora del trabajo de administradores para la planeación de estrategias y logística en la toma de decisiones.


No hay comentarios:
Publicar un comentario